一般の直交座標系とスケール因子
海外の物理数学の教科書やそれに準拠した資料を見てると、球座標のラプラシアンの求め方が日本と違って美しくかつ教育的だったので、それらを参考にしつつ自分なりにまとめてみました。
日本の物理数学および電磁気学の教科書では、大抵が \[\begin{gathered} x=r\sin\theta\cos\phi\\ y=r\sin\theta\sin\phi\\ z=r\cos\theta\end{gathered}\] から、デカルト座標系におけるラプラシアン \[\begin{gathered} \nabla^{2}=\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}}\end{gathered}\]
を愚直に計算していますが、合成関数の偏微分を多用するせいで膨大な三角関数の嵐に見舞われることになります。インターネットで「球座標 ラプラシアン」で検索するとこのやり方で計算している人の資料が何件かヒットするので、やったことがない人は是非一度見て欲しいのですが、その計算量の多さがいかにおぞましいかがよくわかると思います。
以下では、「球座標のラプラシアンを簡単に求める」というテーマのもと、この記事を含む3つの記事に渡り、その方法の基礎となる概念を説明していきます。タイトルは以下の3つにする予定です。
一般の直交座標系
そもそもなぜデカルト座標以外の座標系で考える必要があるのでしょうか。デカルト座標は並進対称性は有りますが、回転対称性はありません。電場が放射状にかつ均等に分布する点電荷の電場を計算するとき、デカルト座標で計算しようとするとかなりめんどうな変数変換をしなければなりません。しかし球座標では回転対称性があるため、積分領域を球面にとったときの計算が容易になります。これは距離が常に一定になるため、距離と偏角についてそれぞれ積分すればいいだけになるからです。このように、対称性の良い座標系を取ると、独立な変数に対して 積分が容易になることが利点として挙げられます。
まずは一般化された直交座標系を考えます。一般化することで、球座標のみならず円筒座標も同様に扱えるようになるからです。これについては後ほど詳しく説明します。
ある座標の基底ベクトル\(\mathbf{e}_{1},\mathbf{e}_{2},\cdots\mathbf{e}_{d}\)が与えられたとき、 \[\begin{gathered} \mathbf{e}_{i}\cdot\mathbf{e}_{j}=0\quad\text{if }i\neq j(i,j=1,2,\cdots,d)\end{gathered}\] が成り立つような座標系、すなわち基底ベクトルが直交するような座標系のことを「直交座標系」と言います。ここでは物理に即した内容を扱うため、3次元かつ基底ベクトルの長さがすべて1であるような座標、正規直交座標系を扱います。
座標変換
3次元空間上の任意の点はデカルト座標系で\((x,y,z)\)と表せます。これを別の変数の組\((u_{1},u_{2},u_{3})\)で表すことを考えましょう。\(x,y,z\)をそれぞれ\(u_{1},u_{2},u_{3}\)で表すのだから \[\begin{gathered} x=x\!\left(u_{1},u_{2},u_{3}\right)\\ y=y\!\left(u_{1},u_{2},u_{3}\right)\\ z=z\!\left(u_{1},u_{2},u_{3}\right)\end{gathered}\] として、\(u_{1},u_{2},u_{3}\)の関数で表すことが出来ます。またこのとき逆も同様に \[\begin{gathered} u_{1}=u_{1}\!\left(x,y,z\right)\\ u_{2}=u_{2}\!\left(x,y,z\right)\\ u_{3}=u_{3}\!\left(x,y,z\right)\end{gathered}\] のように\(x,y,z\)の関数として表現できるものとします。これは単に\((x,y,z)\)と\((u_{1},u_{2},u_{3})\)が一対一対応になっているということを表しています。このような形で表された座標系を一般に曲線直交座標といいます。
微小変位とスケール因子
物理において主に興味があるのは微小量です。ここでは位置ベクトル\(\mathbf{r}\)の微小な変化分\(d\mathbf{r}\)を考えましょう。以降ではこの\(d\mathbf{r}\)を、位置の微小変化という意味で「微小変位」と呼びます。
デカルト座標での位置座標は \[\begin{gathered} \mathbf{r}=x\hat{\mathbf{e}}_{x}+y\hat{\mathbf{e}}_{y}+z\hat{\mathbf{e}}_{z}\end{gathered}\] で表され、微小変位\(d\mathbf{r}\)は \[\begin{gathered} d\mathbf{r}=\hat{\mathbf{e}}_{x}dx+\hat{\mathbf{e}}_{y}dy+\hat{\mathbf{e}}_{z}dz\end{gathered}\] となります。基底ベクトルが位置に依らず変わらないので微小変位の成分がそのまま微分量になっています。しかし曲線直交座標系ではこのようにはなりません。なぜなら基底ベクトルの向きが位置によって変化しうるからです。以下ではこのような場合の取り扱いを説明します。
位置ベクトルを\(\mathbf{r}=\mathbf{r}\!\left(u_{1},u_{2},u_{3}\right)\)と見た時の微小変位は、全微分を用いて \[\begin{gathered} d\mathbf{r}=\frac{\partial\mathbf{r}}{\partial u_{1}}du_{1}+\frac{\partial\mathbf{r}}{\partial u_{1}}du_{1}+\frac{\partial\mathbf{r}}{\partial u_{1}}du_{1}\end{gathered}\] と書けます1。ここで
\[\begin{gathered} \left|\frac{\partial\mathbf{r}}{\partial u_{k}}\right|:=h_{k}\\ \frac{1}{h_{k}}\frac{\partial\mathbf{r}}{\partial u_{k}}:=\hat{\mathbf{e}}_{k}\end{gathered}\]
と定義すると\(d\mathbf{r}\)は更に \[\begin{gathered} d\mathbf{r}=h_{1}\,du_{1}\hat{\mathbf{e}}_{1}+h_{2}\,du_{2}\hat{\mathbf{e}}_{2}+h_{3}\,du_{3}\hat{\mathbf{e}}_{3}\end{gathered}\] と書けます。ここで現れた\(h_{k}\)をスケール因子(scale factor)と言います。上の式は、ある変数\(u_{k}\)を、他の変数は固定しながら\(u_{k}\)を\(du_{k}\)だけ動いたときに、\(\hat{\mathbf{e}}_{k}\)の向きに\(h_{k}du_{k}\)だけ位置ベクトルが変化することを主張しています。
スケール因子の求め方は以下のようにします。デカルト座標で位置ベクトル\(\mathbf{r}=\mathbf{r}\!\left(x,y,z\right)=x\hat{\mathbf{e}}_{x}+y\hat{\mathbf{e}}_{y}+z\hat{\mathbf{e}}_{z}\)が与えられていた場合は以下のようにして求めることが出来ます: \[\begin{aligned} h_{k} & =\left|\frac{\partial\mathbf{r}\!\left(x,y,z\right)}{\partial u_{k}}\right|\\ & =\left|\frac{\partial x}{\partial u_{k}}\frac{\partial\mathbf{r}}{\partial x}+\frac{\partial y}{\partial u_{k}}\frac{\partial\mathbf{r}}{\partial y}+\frac{\partial z}{\partial u_{k}}\frac{\partial\mathbf{r}}{\partial z}\right|\\ & =\left|\frac{\partial x}{\partial u_{k}}\hat{\mathbf{e}}_{x}+\frac{\partial y}{\partial u_{k}}\hat{\mathbf{e}}_{y}+\frac{\partial z}{\partial u_{k}}\hat{\mathbf{e}}_{z}\right|\\ & =\sqrt{\left(\frac{\partial x}{\partial u_{k}}\right)^{2}+\left(\frac{\partial y}{\partial u_{k}}\right)^{2}+\left(\frac{\partial z}{\partial u_{k}}\right)^{2}}\end{aligned}\]
具体例として2次元極座標を考えてみましょう。
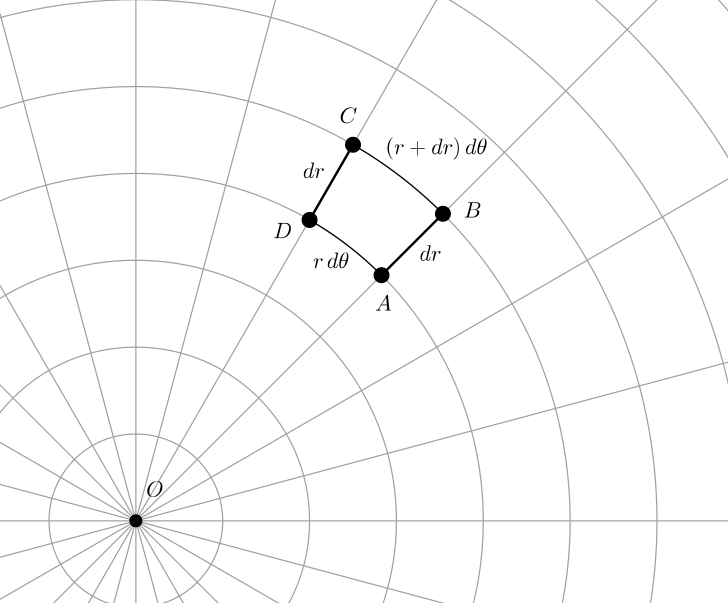
上の図は極座標を動径\(r\)、偏角\(\theta\)を一定間隔で区切ったときの模式図を表しています。この間隔を微小量\(dr\)とみなします。(本来\(dr\)は図に表せないほど小さいのですが、わかりやすくするためわざと大きく書いています。)
図からもわかるように、\(\theta\)を一定にして\(dr\)だけ動かすと、AD間の距離は\(dr\)になっています。また\(r\)を一定にして偏角を\(d\theta\)だけ動かすとBC間の距離が\(r\,d\theta\)になっています。また、この場合のスケール因子\(h_{r},h_{\theta}\)はそれぞれ\(1,r\)です。
この例からも分かる通り、スケール因子を扱う一番の大きなメリットは、ある変数のみを微小量だけ動かした時の微小変位の長さが容易に求まることに有ります。例えば微小変位の距離の2乗\(ds\)は \[\begin{gathered} ds^{2}=d\mathbf{r}\cdot d\mathbf{r}\\ =\left(h_{1}\,du_{1}\hat{\mathbf{e}}_{1}+h_{2}\,du_{2}\hat{\mathbf{e}}_{2}+h_{3}\,du_{3}\hat{\mathbf{e}}_{3}\right)\cdot\left(h_{1}\,du_{1}\hat{\mathbf{e}}_{1}+h_{2}\,du_{2}\hat{\mathbf{e}}_{2}+h_{3}\,du_{3}\hat{\mathbf{e}}_{3}\right)\\ =\left(h_{1}\,du_{1}\right)^{2}+\left(h_{2}\,du_{2}\right)^{2}+\left(h_{3}\,du_{3}\right)^{2}\end{gathered}\] となりますし、更に微小体積の計算も、基底が直交していることから、基底の成分をそれぞれ掛け合わせるだけでよく、 \[\begin{gathered} dV=h_{1}h_{2}h_{3}\,du_{1}du_{2}du_{3}\end{gathered}\] となります。これはヤコビアンそのものです。
一般の直交座標の成す曲線群は、歪んだ格子状になっています。この歪み分が、(微小変位の成す距離)\(\neq\)(座標の微小変化)となる直感的な理由です。この点がデカルト座標と一般の曲線直交座標における大きな違いであり、難しさでもあります。しかしこのような座標系を扱うことによって、対称性の良い座標系を選んで積分する操作を偏微分やヤコビアンを直接計算せずに行えるというメリットの大きさは、計算の簡略化という点において計り知れません。また次の記事で言及するように、デカルト座標上における演算子を定義として偏微分などの作業から形式的に書き換える作業も避けることが出来ます。これもまた大きなメリットであるとともに、演算子の形を記憶する際の手助けにもなるでしょう。最後に、球座標と円筒座標についての座標変換とスケール因子を表にまとめておきます。

次はベクトル解析について書く予定です。
参考文献
1 http://akita-nct.jp/yamamoto/study/electromagnetics/coodinate_transform/coodinate_trans.pdf
自分がこの題材を勉強するにあたって最初に参考にした資料です。丁寧かつ非常にわかりやすいので是非読んでみてください。
2 https://en.wikipedia.org/wiki/Orthogonal_coordinates
\(\left|\dfrac{\partial\mathbf{r}}{\partial u_{k}}\right|=h_{k}\)という表記はここを参考にしました。ただしこの記事では一般座標を\(q^{k}\)ではなく\(u_{k}\)としています。
-
ベクトルの全微分も、スカラー量の全微分と同様にして定義することが出来ます。すなわちスカラー関数\(f\!\left(u_{1},u_{2},u_{3}\right)\)の偏微分が\(\frac{\partial f\!\left(u_{1},u_{2},u_{3}\right)}{\partial u_{1}}:=\lim_{\Delta u_{1}\to0}\frac{f\!\left(u_{1}+\Delta u_{1},u_{2},u_{3}\right)-f\!\left(u_{1},u_{2},u_{3}\right)}{\Delta u_{1}}\)で定義されたように、ベクトルの偏微分も\(\frac{\partial\mathbf{r}\!\left(u_{1},u_{2},u_{3}\right)}{\partial u_{1}}:=\lim_{\Delta u_{1}\to0}\frac{\mathbf{r}\!\left(u_{1}+\Delta u_{1},u_{2},u_{3}\right)-\mathbf{r}\!\left(u_{1},u_{2},u_{3}\right)}{\Delta u_{1}}\)というように定義可能です。↩